Participate Media

Heterogeneous Participating Media (30 points)

Relevant code:

• include/kombu/medium.h
• include/kombu/phase.h
• include/kombu/volume.h
• src/mediums/homogeneous.cpp
• src/mediums/heterogeneous.cpp
• src/phase/isotropic.cpp
• src/volumes/constvolume.cpp
• src/volumes/gridvolume.cpp
• src/integrators/vol_path_mats.cpp
• src/integrators/vol_path_mis.cpp

Since we created chimneys with smoke on the house, I implemented heterogeneous participate medium. I start this by implementing a HomogeneousMedium class with simple path tracing integrator vol_path_mats. Note that our medium can be only attached to a specific shape. This is achieved by adding free path sampling and phase function sampling to the path_mats when the origin of current recursive ray is in the medium. Besides, the three channels color information is considered in the homogeneous medium. After that, I implemented a more complex vol_path_mis integrator , which extends the path_mis integrator. This integrator is tricky because we need to consider:

• Correctly calculate the MIS weight (for medium and surface cases), and normalize the weight for delta sampling.
• Recursively check the shadow ray intersection, multiply the transmittance if the ray go through a medium.
• Recursively check the emitter intersection.

Then, the HeterogeneousMedium is implemented with the Volume data structure. Currently there are two types of volume : ConstVolume and GridVolume. The later one can read the same data format as mitsuba with the help of the external libray Qt4.

Validation:

1. Homogeneous medium and vol_path_mis integrator:
As shown in the following figure (cbox with 128 samples per pixel), the vol_path_mis integrator has better performance than the vol_path_mats integrator. And our integrator has similar result compared to mitsuba (our noise is even smaller than mitsuba). The parameters are:
Left ball: $$\sigma_t = (6, 3, 2), albedo = (0.167, 0.333, 0.5)$$ Right ball: $$\sigma_t = (2, 3, 6), albedo = (0.5, 0.333, 0.167)$$

The comparison with different scattering coefficient is shown below:
No scattering: \(albedo_l = albedo_r = (0, 0, 0)\)
Full scattering: \(albedo_l = albedo_r = (1, 1, 1)\)

Besides, our integrator can pass all the previous tests:
test-furnace

Generating 100000 paths.. 
Sample mean = 5.02035 (reference value = 5)
Sample variance = 8.1692
t-statistic = 2.25163 (d.o.f. = 99999)
Accepted the null hypothesis (p-value = 0.0243476, significance level = 0.00250943)

Passed 4/4 tests.
                

test-direct

Generating 100000 paths.. 
Sample mean = 0.261954 (reference value = 0.26174)
Sample variance = 0.0195052
t-statistic = 0.484854 (d.o.f. = 99999)
Accepted the null hypothesis (p-value = 0.627781, significance level = 0.00100453)

Passed 10/10 tests.
                

2. Heterogeneous:
As shown in the first figure, the heterogeneous medium with ConstVolume has the same result as our homogeneous participating medium. And as shown in the second figure, GridVolume has the similar result as mitsuba.

Different distance sampling (transmittance) estimation methods (10 points)

Relevant code:

• src/mediums/heterogeneous.cpp

I also implemented different methods for free path sampling and transmittance estimation. Note that transmittance is used when calculating the recursive shadow ray to the emitter. For delta tracking and ratio tracking, the free path sampling methods are the same (i.e. use the majorant density to sample the distance, then use the real density for rejection). However, the transmittance estimation is slightly different. For delta tracking, the transmittance is estimated using a \(0-1\) distribution of passing through the meidum, and for ratio tracking, we multiply the ratio of fictitious density and majorant density \(1 - {\sigma_t(x) \over \bar \sigma_t}\) for each majorant sampling step, because this is the probability of passing through this sample (no rejection).

For ray marching, similar to Mitsuba, I use Simpson quadrature to compute the integral: $$ integral = \int_{ray.mint}^{ray.maxt} \sigma_t(ray(x)) dx $$ For transmittance estimation, we simply use the \(e^{-integral}\) as the transmittance. And for free path sampling, I integrate the density until: $$ \int_{ray.mint}^{t} \sigma_t(ray(x)) dx > -ln(1- \xi) $$ Then, Lagrange polynomial is used to find the specific point such that the equality is held.

Validation:

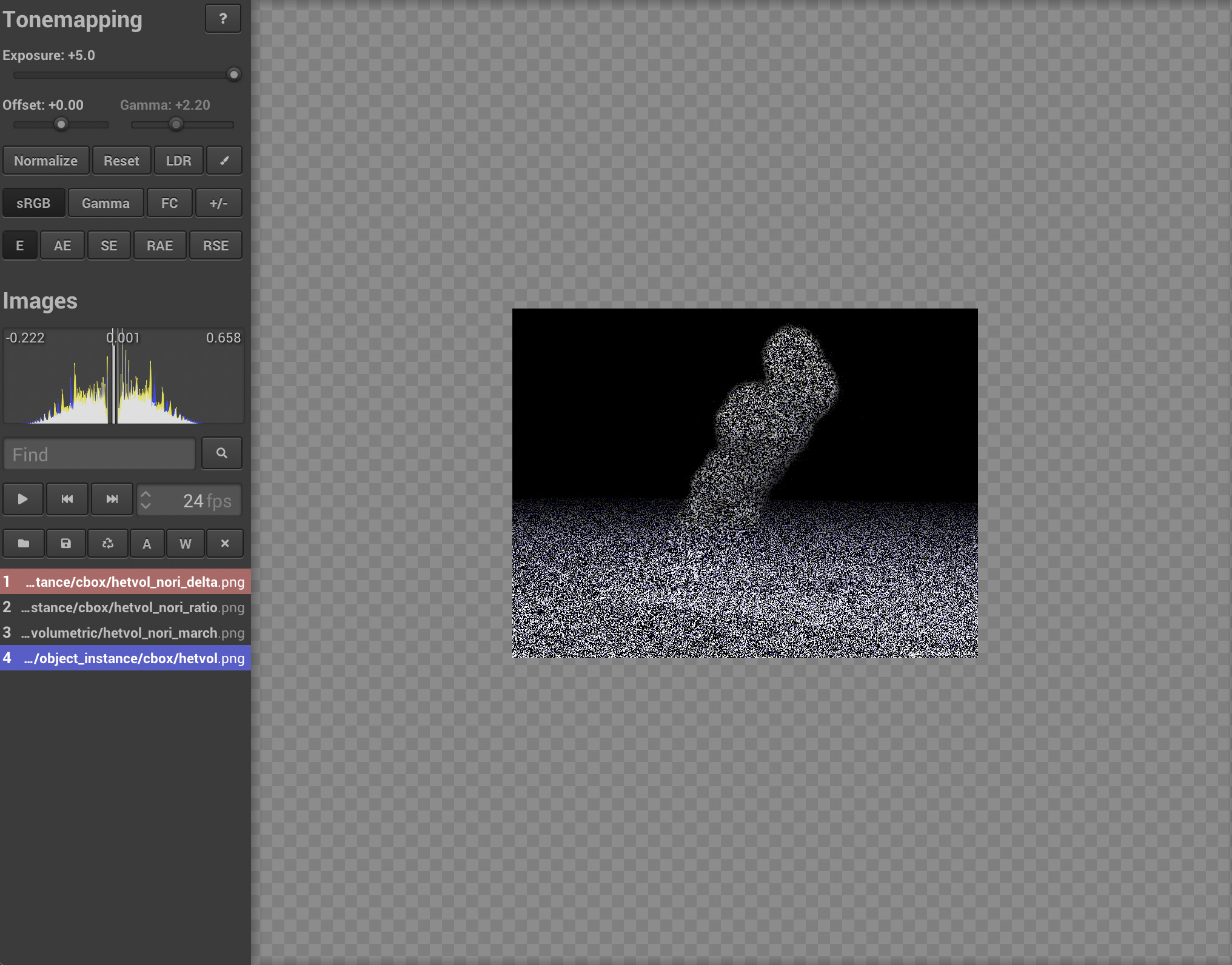
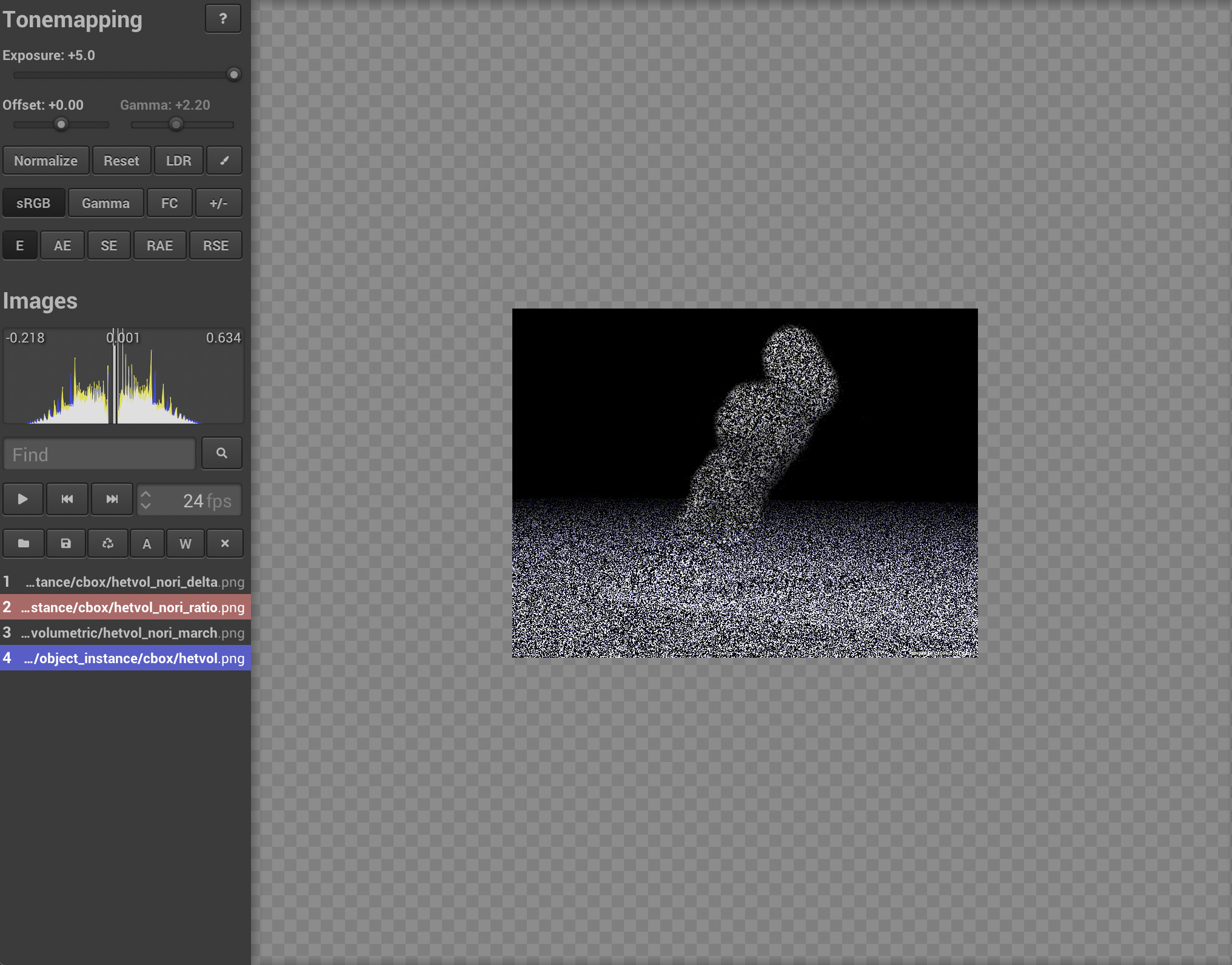
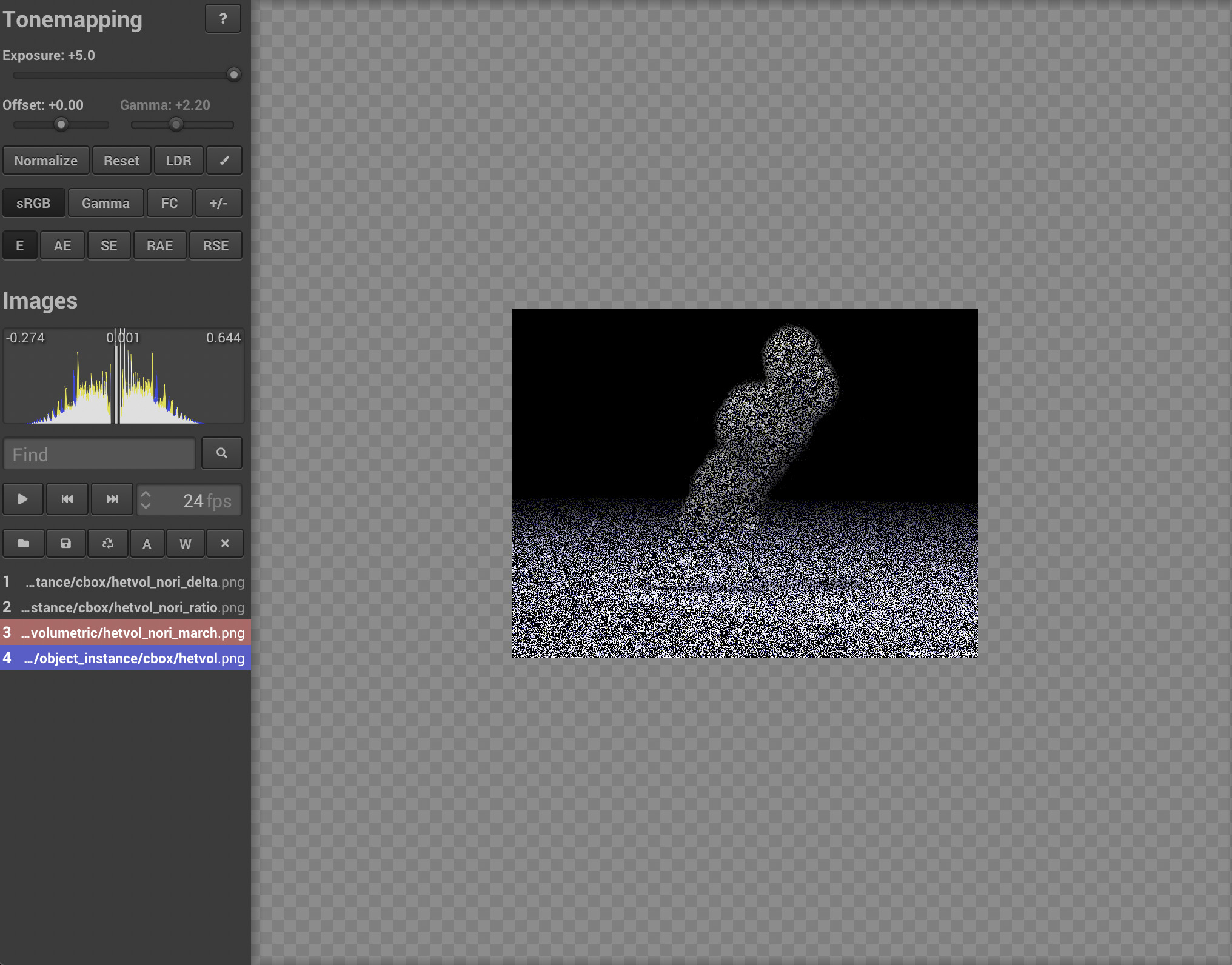
As shown in the validation for heterogeneous medium (the smoke), our delta tracking has the similar result as mitsuba. The following figure shows our ray marching result compared with mitsuba. Note that since transmittance is only used for shadow rays, we only need to observe the shadow of the smoke.

Since mitsuba doesn't implement ratio tracking, I validate this feature by showing it has smaller variance. The following figure compares the ray marching, ratio tracking and delta tracking with sampling per pixel 32. As expected, ratio tracking performs slightly better than delta tracking. And ray marching has better performance in the shadow part. This is because ray marching uses more samples for transmittance integration compared with unbiased methods.

The following image shows the error metric between our three methods and mitsuba result. Note that the mean error \(0.001\) comes from the right bottom corner logo of mitsuba render. The variance is a little bit lower for ratio tracking compared with delta tracking. Since the ray marching is a biased estimator, mean of the error distribution is shifted compared with other two methods. We can still find that the shadow part of ray marching is better than other two methods.

Anisotropic Phase Function (5 points)

Relevant code:

• include/kombu/phase.h
• src/phase/hg.cpp
• src/sample/warp.cpp
• src/tests/warptest.cpp

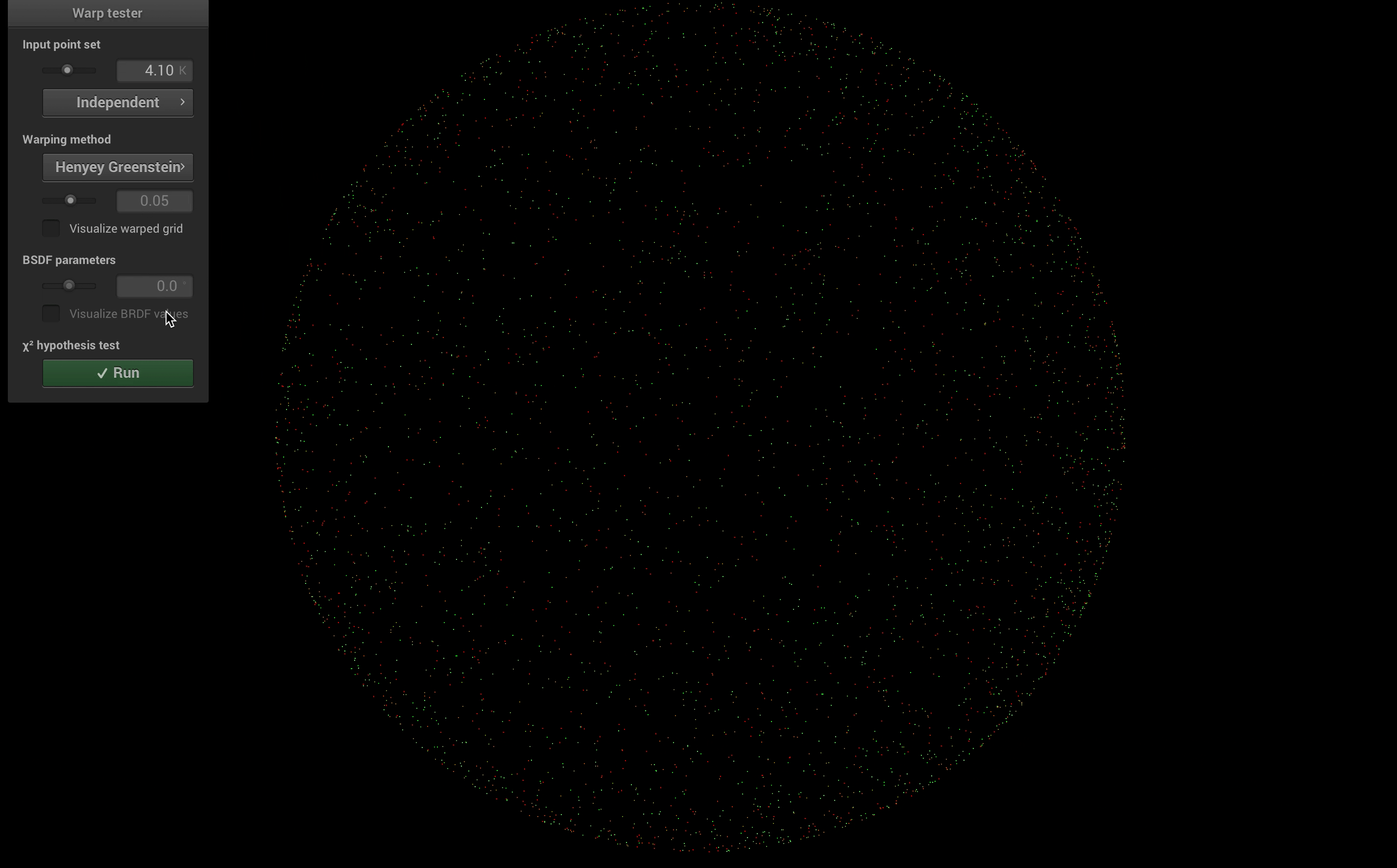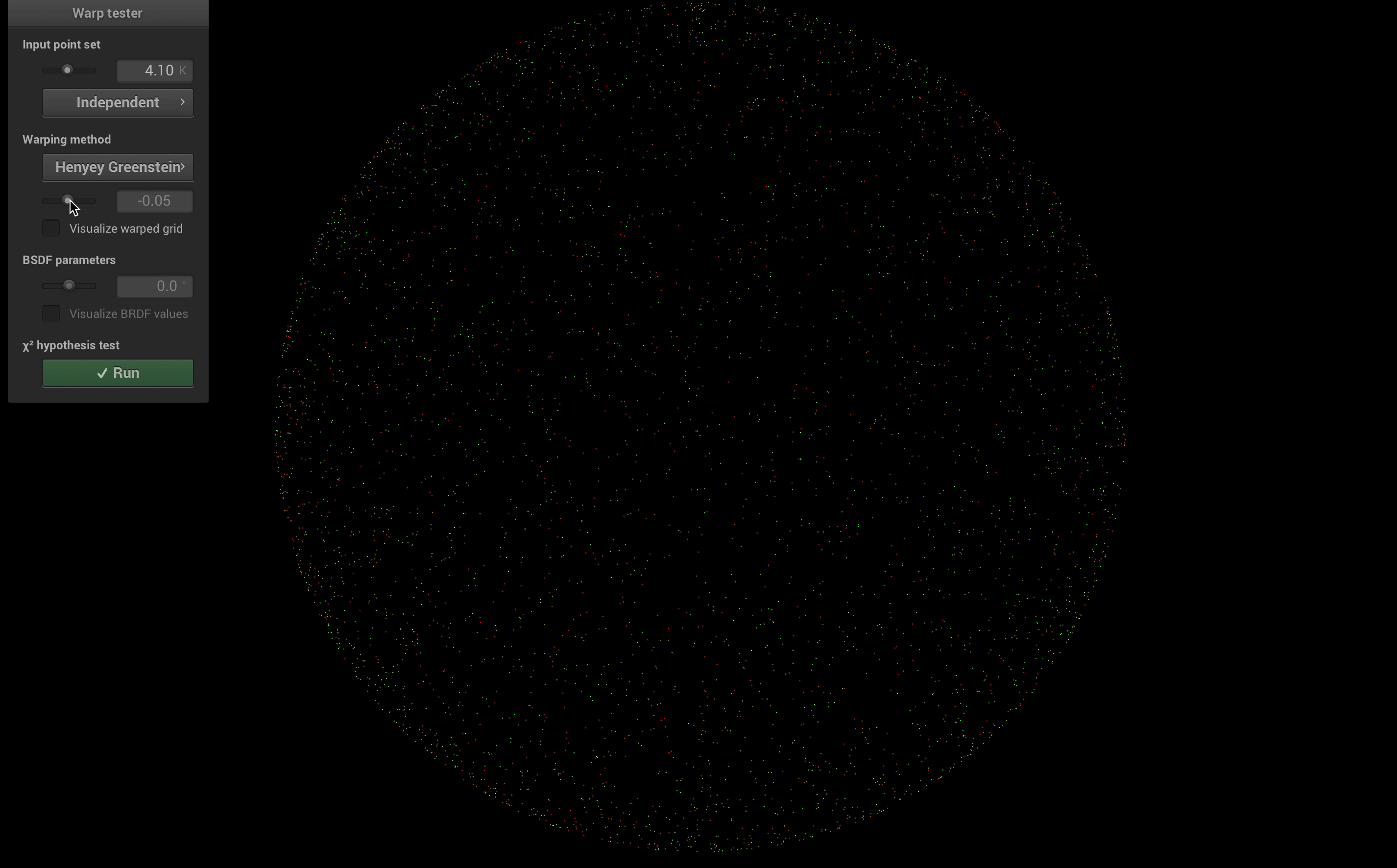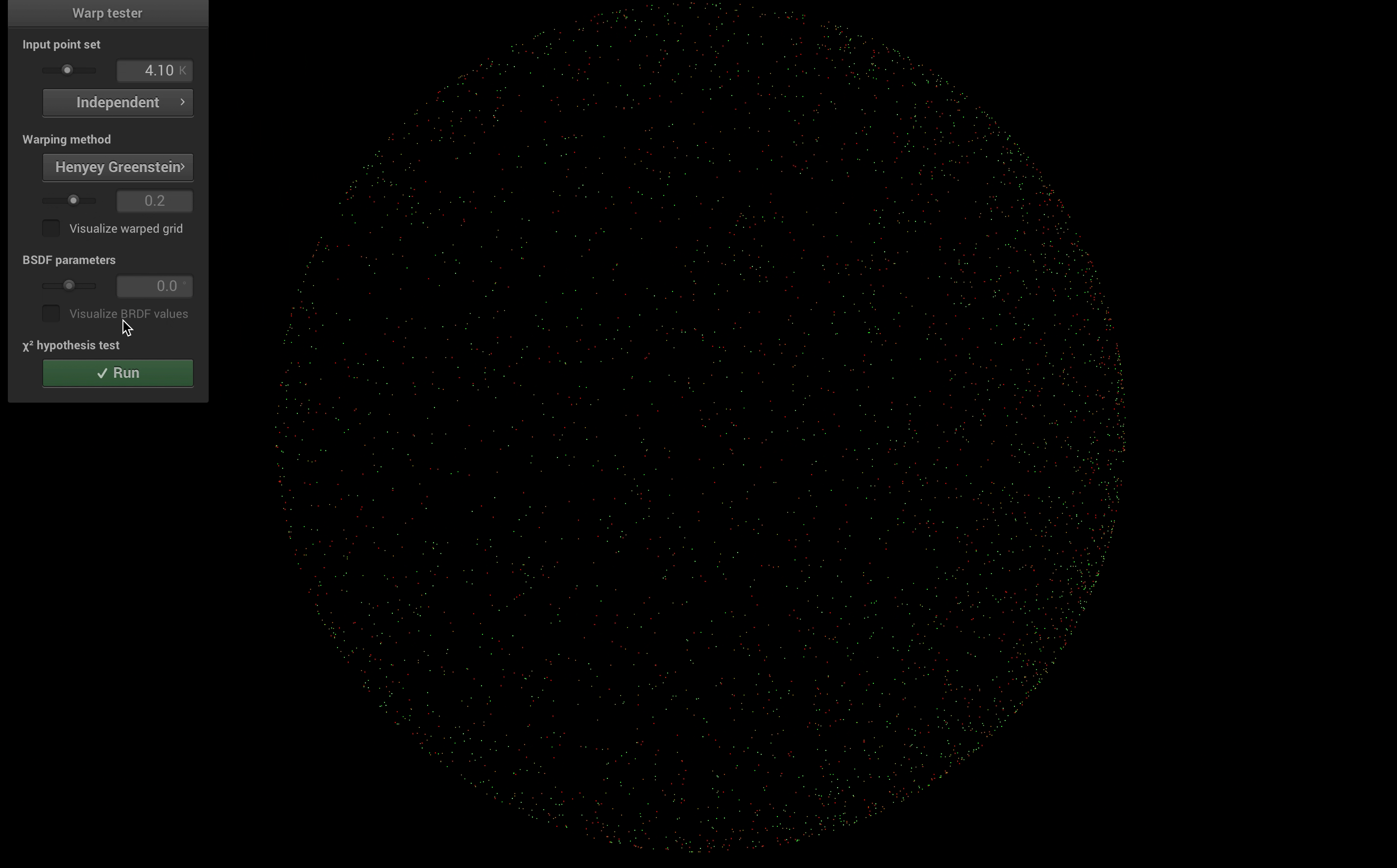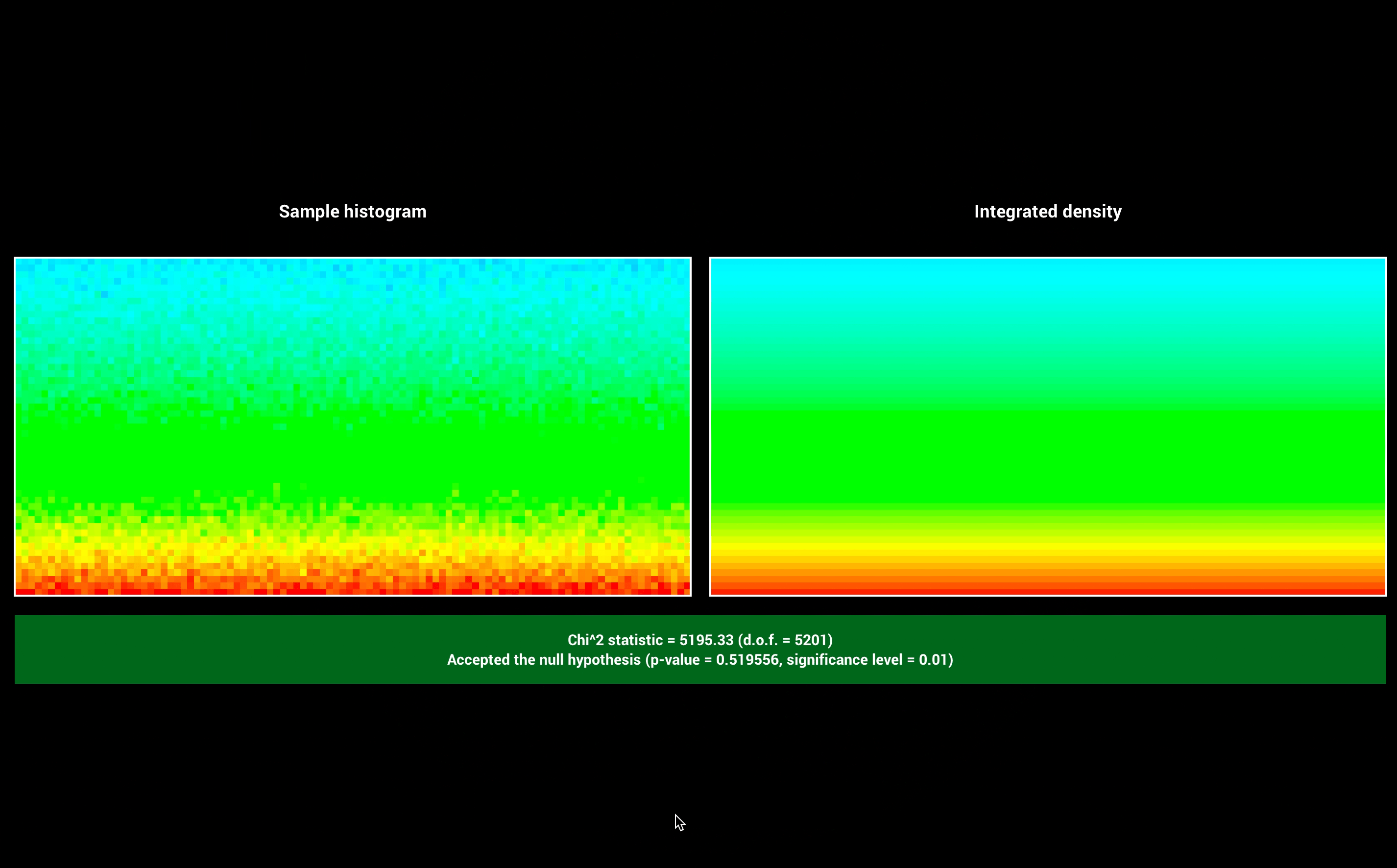
For Henyey-Greenstein phase function, I implemented a new sampling method in the warp.cpp, and a new phase function class. I also implemented a warptest to validate the result.

Validation:

As shown in the following image, all the parameters are the same as previous tests, the only difference is that, for the left ball \(g = 0.5\), and for the right ball \(g = -0.5\). The following figure shows a comparison between our implementation and Mitsuba. Our methods have similar performance as mitsuba, even better in terms of noise.

Besides, the result of warp test is shown below:

Basic Denoising: Bilateral Filter with Uniform Variance (5 points)

Relevant code:

• include/kombu/denoiser.h
• src/utils/bilaterial.cpp
• src/utils/nl_means.cpp
• src/core/render.cpp

For denoiser, I implemented basic bilaterial denoiser as well as NL means denoiser with uniform variance. Since NL means preserves better structure information, it is used for validation. The idea is to compute patch-wise color distance and report distance around the center pixel and use its exponential as weight to filter the image.

Validation:

As shown in the following image, our denoiser can reduce the noise. Used in conjunction with our stratified sampler, the performance is much more better than the individual sampling without denoising.

The following figure shows that the variance of the error is reduced after denoising after stratified sampling and denoising:

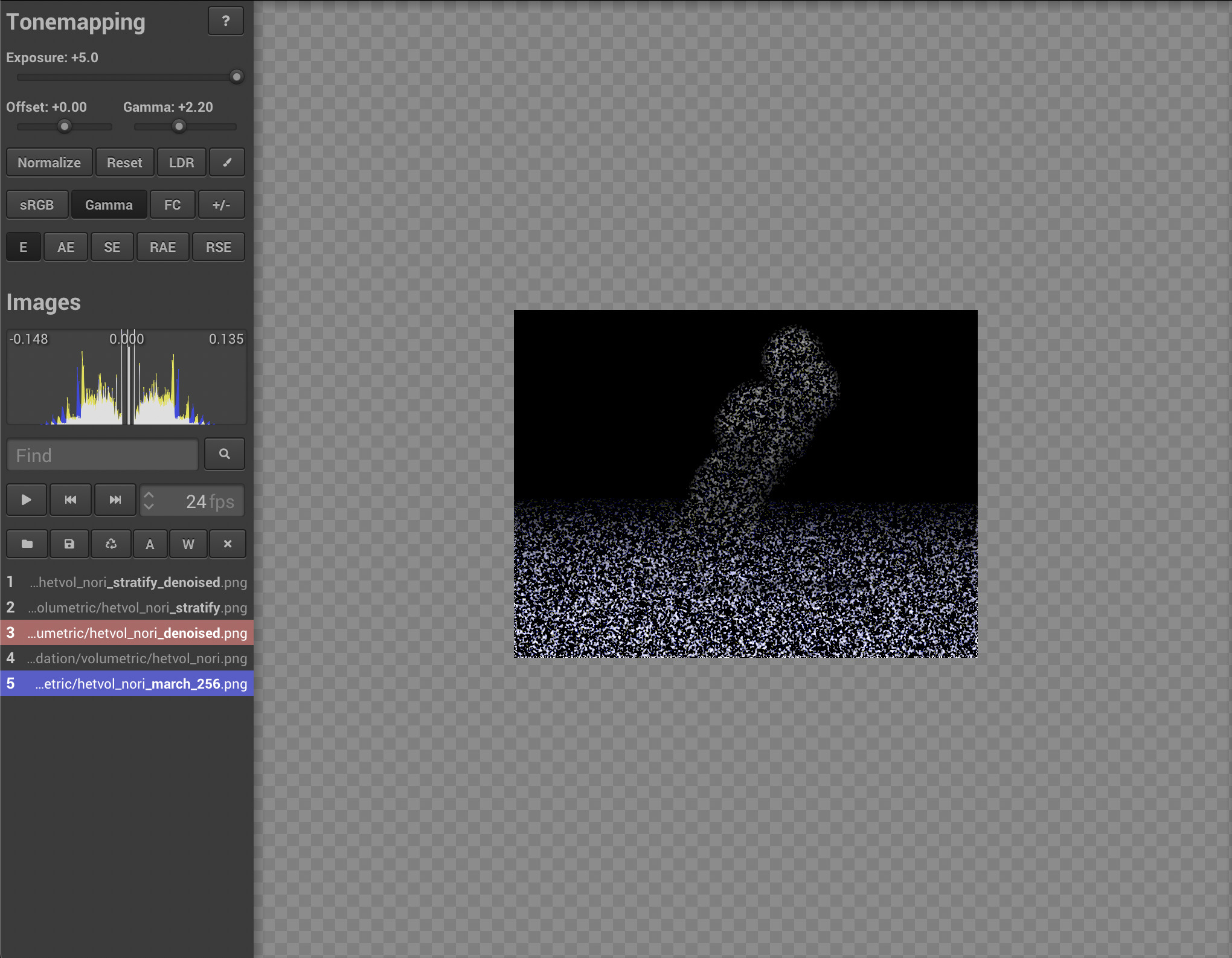
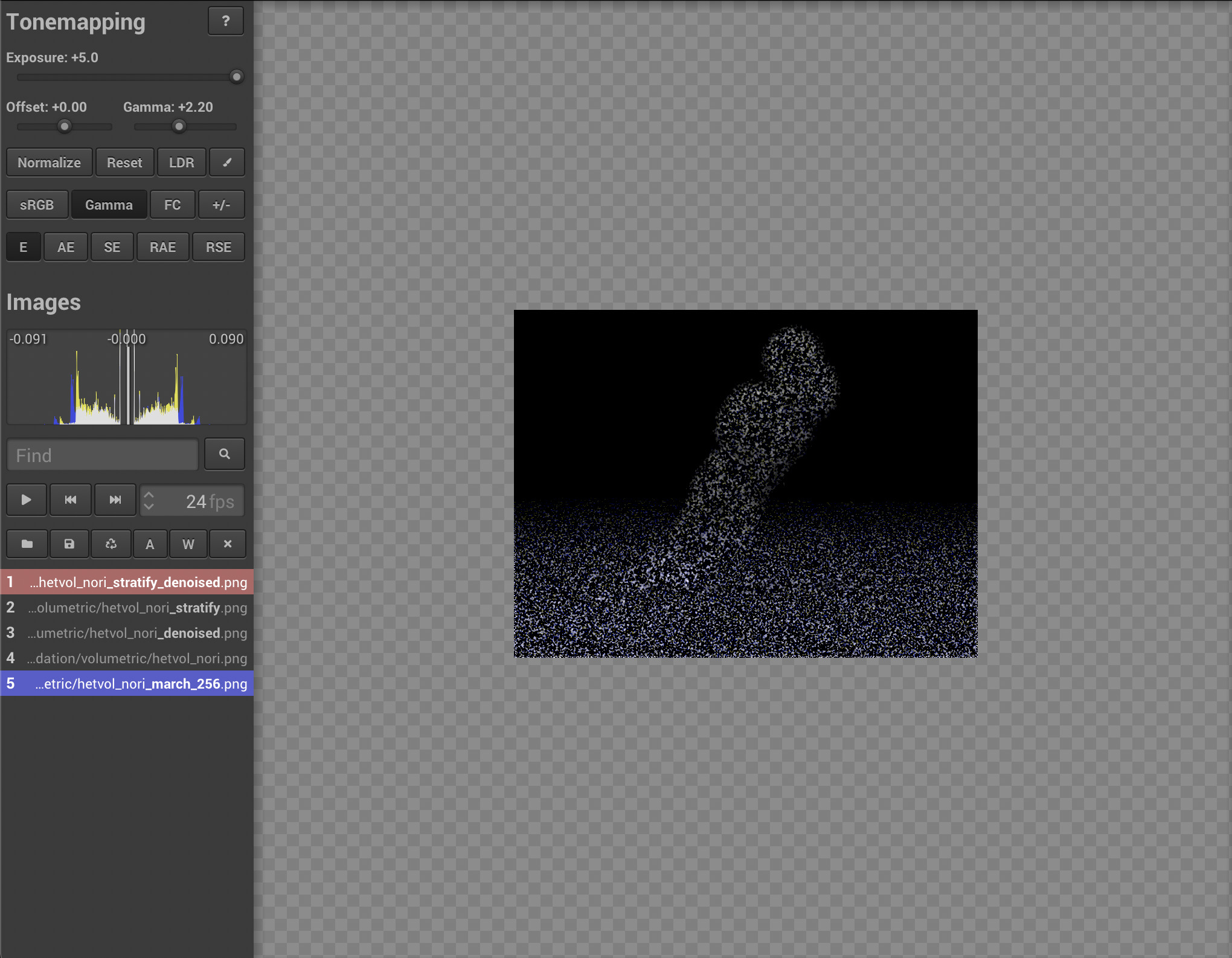
Simple Extra Emitters: directional light (5 points)

Relevant code:

• src/emitters/directional.cpp
• src/integrators/direct_ems.cpp
• src/integrators/direct_mis.cpp
• src/integrators/path_mis.cpp
• src/integrators/vol_path_mis.cpp

For directional light, the eval() and pdf() methods are trivial, since it is a delta light (just return 0 and 1). However, in order to calculate the transmittance between the emitter and the query point, we need to assign a 3D point in the sampling function. We first get the bounding sphere of the scene, and find the intersection of the directional light direction starting from the center of the sphere. Then we project the vector from the query point to the intersection point to the directional light direction. The projected point is used as the point for light sampling. Although it is not an accurate solution, but it is more efficient.
Another tricky issue is that for MIS, similar to the delta BSDF, the delta light is impossible to be hit by the ray sampled by BSDF. Therefore, we normalize the \(w_{ems} = 1, w_{mat} = 0\) for delta light.

Validation:

As shown in the following figure, our directional light works well with different light direction, and has the same result as mitsuba:

Object Instancing (5 points)

Relevant code:

• include/kombu/instance.h
• include/kombu/reference.h
• src/geometry/instance.cpp
• src/geometry/reference.cpp
• src/core/scene.cpp

For the object instancing, I implement one object (shape class) instancing without shape group (since the multiple intersection checking is a bit tricky). My implementation cannot add child to instance, but only allow the transformation of the reference object. For all instances that point to the reference object, all geometry operations are transformed to the local frame of the instance and call the corresponding function in the reference object.

Validation:

I compare the result of object instancing with the result using two seperate spheres, these two cases should have the same output image. Also, I show the spheres with texture to prove the rotation is correct.